こんにちは、小俣です。
下吉田中生の皆さん、いよいよ来週です。課題は仕上がってますか。ちょうど一週間前ですので、今日から2回目・3回目が理想なのですが。いづれにせよ、終わり切りましょうね
本日は、
小学生 英検クラス16時30分 国語・算数17時20分から
中1生・中2生・中3明見中・富士見台中 19時20分からです。
中 1 生 明 日 で す 。 頑 張 り ま し ょ う ! !
こんにちは、広見校の深澤です。
ロングスリーパーで有名な私ですが、本日珍しく早起きをしました。
なぜかって?某ハンバーガーチェーン店の、幸せセットを買うためです(^^;
最近ハマっているキャラクターの幸せセットが今日から発売で、大人気だから出勤前に行かなくては…!と思い向かいましたが、私のほかにお客さんはほとんどいませんでした(笑)
無事にコンプリートできて、ルンルンでブログを書いています(^^♪
前日に安廣先生にこの話をしたら、「深澤先生こういう時の行動力すごいからなあ」と言われてしまいました(笑)
行動力といえば、最近広見校の生徒の間で、素晴らしい行動力の子が増えているのです。
その名も週5文理!!(週6文理の猛者もたまにいます)
週3回の授業に加えて、週2回自習にくる子が増えています!!
実は、じわじわと中2の間で流行しています。
この行動自体十分素晴らしいのですが、何が本当にすごいかというと、これ、生徒たちが自主的に行っているんです!!すごくないですか!?
テスト前など関係なく、自分たちで友人を誘って週5文理をしています!!
また、授業中にわからないところがあると、「明日自習にくるからここもう一回教えて!」と、その場で補習の予約をしてくる子もいましたね。
大人たちに言われる前に自分から行動する子どもたちはきっと伸びますよ。これからの成長が本当に期待されます。
授業のない日でも、校舎が開いている日なら自習室使い放題、質問し放題の学習塾は文理学院です。
成長に夏に向けて、文理で一緒に勉強しませんか?
お気軽にお問い合わせください。
文理学院 広見校TEL 0545-22-5055
こんにちは、鎌矢です。
皆さんは、ゲーム画面のオブジェクト配置と正弦定理の関係について、普段からどう考えていますでしょうか。2つの円の交点が合計2つ出てくるので計算が厄介だな~など思考を巡らしているでしょうかね。…おや?何の話しているか分からないよ、という表情していますか?そんなまたまた…
というわけで、今回はずいぶんと狭い狭い話、ゲーム画面とカメラの画角の話をしましょう。オタッキー!これは、私がゲーム画面におけるプレイヤーとターゲットの位置関係とカメラ位置について考えていた時のことです。画面構想としては3Dゲームで以下の状態です。あ、正弦定理は1年生の数学Ⅰ「図形と計量」の範囲ですよ。
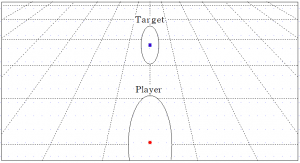
自分がPlayer、目標がTargetで、カメラ位置を考えていました。カメラ位置の構想として、Playerの頭上の少し後ろに配置され、双方が画面に図のように収まるような位置です。この画面の位置関係ならばそう難しくはなさそうですが、PlayerとTargetの位置関係が変化し、二人の距離や、高低差が変化した時にも同じような画面状態を維持したい、という前提のもとカメラ位置を特定する必要があります。そこで、カメラ位置から、対象へと直線を伸ばした時の、成す角について考えることにしました。
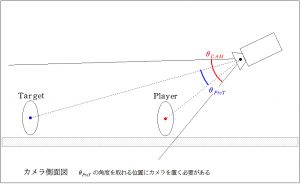
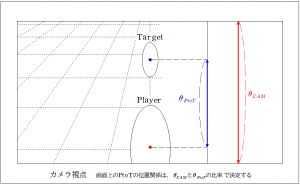
カメラには視野角(カメラが写せる範囲)があり、その視野角によって画面の縦方向の表示される広さ、すなわち縦方向の角度が決定します。この角度をθCAMとしましょうか。角度が画面上の長さを決定づけるようですね。ならば、このPlayerとTargetの位置関係も、画面上の縦方向の距離関係なので、画面内の距離を維持したいというならば、角度を維持するということになるはずです。ですので、θPtoT(PlayerからTarget)として、この角度を固定する、という設計になりました。とりあえず、30°とします。なので、カメラ位置については、二人をなす角30°で覗ける位置に配置となりました。
さて、二人を30°で覗ける位置を計算で求めたいのですが、この前提を満たす位置、どのあたりにあるでしょうか…と考えたとき、とりあえず、図をかきました。PlayerとTarget、そしてそれをなす角30°で覗くカメラ…三角形ですね。この三角形について、ほかに算出できるものは、PtoTの距離だけなのですが、ここの距離と角度30°の位置関係は、どこかで見たことがある気がします。a/sinA…正弦定理の配置ですね。一辺とその対角を用いた三角比の公式で、a/sinA=2R。つまり外接円の半径が決定するのです。というわけで、下の図、左。30°で覗ける位置は、青の円上となるはずです。(実際は円の下は150°であり対象外、また下にも一つ円が描け、それも条件を満たす)確かに30°を維持するのは円周角の定理からわかります。この円上がカメラが位置する必要条件です。
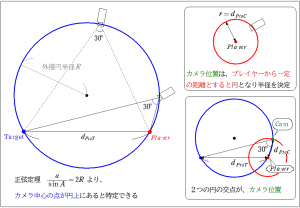
あとは、カメラの位置条件に追加します。プレイヤー付近の位置とするために、一定距離の位置、つまりPlayer中心の円とすると、カメラその円上にも位置することになります。つまり、2つの円の交点上が答えです。 …というわけで、これにて設計完了です…おや?何の話をしているのか分からないよ~という表情…?
というわけで、画面構成とカメラ位置と正弦定理の話でした。…人生で正弦定理が関わるなんて、高校生時代の私には想像できませんでした… 当時は受験の為でしたが、知識ってこんなところで急にでてくるんだなぁ、という話でした。
都留校 小澤です。
本日5/16 (金) は、昨日までの欠席者補習を行います。
※ 中学3年生の5/15 (木) の授業は英和中のみ対象なので、それ以外の中学校の生徒さんの欠席補習授業はありません。
🌟 おまけ 🌟
個人的なお話になりますが、私、ただいま引っ越しをしています。
のんびりとやっているのですが、いよいよ大詰めといったところで、足りない生活品などを買いそろえている段階です。
うちの家族は「ニトリ」さんが好きなようですが、私は「アマ〇ン」さんに頼りきっています。
ありとあらゆるものをアマ〇ンさんで購入しているので、中には配送された商品が間違っていた事もあります。
型番違いの家電製品が届きました。見た目で判断するのは難しい事例でしたが、たまたま説明書に表記されているスペックの違いに気づき、事なきを得ました。
もし、間違いに気づくのが遅れていたら、伝票はもちろん、商品のパッケージまでもグチャグチャにして捨てちゃいますから、返品はできなくなります。気をつけなきゃですね!
まぁ、明らかに違うものが入ってたらそりゃ気づきますけど・・・ (;´∀`)
そして、うちの娘に頼まれていた商品 (つっぱり棒) が届くはずでした。
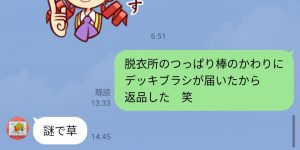
みなさんも、商品購入の際には、きちんと確認をしてくださいね~ 笑
こんにちは。唐瀬校舎の千葉です。
昨日5/14、本日5/15と市立高校と城北高校の生徒は翌日の中間テストに向けちょくぶんの日でした。あと1日頑張ってください。「もう、テストうけたくないです~。」(+o+)と言っていた市立高校1年のAさんもしっかりちょくぶんして偉かったです。
校舎のオープンとともに生徒が来て、お昼ご飯を食べています。「結構、まんま出題されてた!」(^o^)丿と言う城北高校のBさんは翌日の英語に向けて音読からスタートです。
高校1年生は初めてのちょくぶん。部活がある生徒も終わり次第来ていました。
こちらは夜の自習室、静高、東の生徒は夕方から夜にかけて自習をしています。来週は月曜から校舎を13時にオープンしますので、勉強しに来てください。