こんにちは、鎌矢です。

皆さんは、ゲーム画面のオブジェクト配置と正弦定理の関係について、普段からどう考えていますでしょうか。2つの円の交点が合計2つ出てくるので計算が厄介だな～など思考を巡らしているでしょうかね。…おや？何の話しているか分からないよ、という表情していますか？そんなわけ…

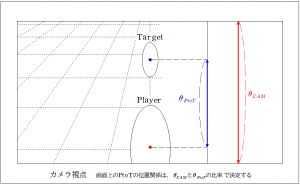
はい、というわけで、今回はずいぶんと狭い狭い話、ゲーム画面の画角の話をしましょう。これは、私がゲーム画面におけるプレイヤーとターゲットの位置関係を考えていた時のことです。画面構想としては以下の状態です。あ、３Dゲームの話です。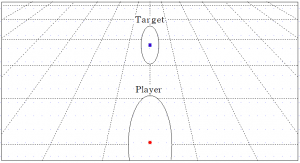自分がPlayer、目標がTargetで、カメラ位置を考えていました。位置の構想として、Playerの頭上の少し後ろから、双方が画面に図のように収まるようなカメラ位置です。この画面の位置関係ならばそう難しくはなさそうですが、PlayerとTargetの位置関係が変化し、二人の距離や、高低差が変化した時にも同じような画面状態を維持したい、という前提のもと、カメラ位置を特定する必要があります。そこで、カメラ位置から、対象へと直線を伸ばした時の、成す角について考えることにしました。

カメラには視野角(カメラが写せる範囲)があり、その視野角によって画面の縦方向の表示される広さ、すなわち縦方向の角度が決定します。この角度をθCAMとしましょうか。角度が画面の長さを決定づけるようですね。ならば、このPlayerとTargetの位置関係も、画面上の縦方向の距離関係なので、画面内の距離を維持したいというならば、角度を維持するということになるはずです。ですので、θPtoT(PlayerからTarget)として、この角度を固定する、という設計になりました。とりあえず、30°とします。なので、カメラ位置については、二人をなす角30°で覗ける位置に配置となりました。

さて、二人を30°で覗ける位置を計算で求めたいのですが、この前提を満たす位置、どのあたりにあるでしょうか…と考えたとき、とりあえず、図をかきました。PlayerとTarget、そしてそれをなす角30°で覗くカメラ…三角形ですね。この三角形について、ほかに算出できるものは、PtoTの距離だけなのですが、この距離と角度30°の位置関係は、どこかで見たことがある気がします。a/sinA…正弦定理の配置ですね。一辺とその対角を用いた三角比の公式で、a/sinA=2R。つまり外接円の半径が決定するのです。というわけで、下の図、左。30°で覗ける位置は、青の円上となるはずです。(実際は円の下は150°であり対象外、また下にも一つ円が描け、それも条件を満たす)確かに30°を維持するのは円周角の定理からわかります。この円上がカメラが位置する必要条件です。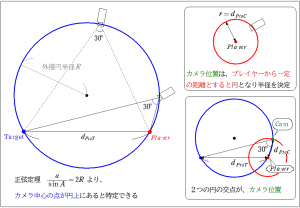あとは、カメラの位置条件に追加します。プレイヤー付近の位置とするために、一定距離の位置、つまりPlayer中心の円とすると、カメラその円上にも位置することになります。つまり、2つの円の交点上が答えです。　…というわけで、これにて設計完了です。ふう…話しきったぜぇ…おや？何の話をしているのか分からないよ～という表情…？

というわけで、画面構成とカメラ位置と正弦定理の話でした。…人生で正弦定理が関わるなんて、高校生時代の私には想像できなかったなあ…　使う場面が想像できない知識も、いつか役に立つかもです。テストを期に、知識を育んでいきましょう。実際こんな設計現場でやってるのかな…？

そいで今は、定期テスト！もう始まっているところもある！定期テストの荒波の中、全力でぶつかっていきましょう！