都留本部校『土曜日です。明日から中3特訓です！』2025.8.9①

都留校小澤です。

本日8/9 (土) は、中3夏期講習、中学生Be-Wing夏期講習＋通常授業となります。
そして、明日からは中3教達検特訓です！ (*‘∀‘)/
※ 夏期講習生は「教達検特訓への申込者のみ」となります。
大月校へ現地集合です。お昼ご飯 🍚🥢 を持ってくるようにしてください。ご不明な点は本日中なら都留校 (0554-43-1403) へ、明日あさっては大月校 (0554-23-3786) へお願いします。

🌟 おまけ 🌟
夏期講習『理数科合格クラス』へ参加している人へ向けてです。
先日のブログでの数学難問『問2 (2)』のお話です。うわさでは「正答率0.1％の問題」との事ですが、さすがN村さんは『相似』を使って解ききったようです！ (*’ω’*)

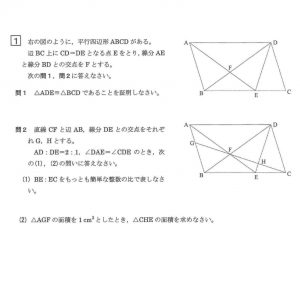
私も私なりに考えてみました。 (;´∀｀)
△AGFの面積がわかっているので、△AGFと△CHEの底辺と高さのそれぞれの比がわかれば良さそうです。
※ 長さではなく、長さの比のまま解いていく問題です。(1) の『BE:EC＝3:1』を使っていこうと思います！
△AGFの底辺をAGとすると、高さはFから直線AGに下した垂線の長さになりますが、もう一方の△CHEの底辺をECとして考えようと思うので、ECに平行なF-AGの長さがわかれば良さそうです。同様に AGに平行なH-ECの長さも求めようと思います。三平方の定理などを使っての「線分に対しての垂直な長さ」を計算しなくとも行けそうです！ (*‘∀‘)/ では解析開始です～

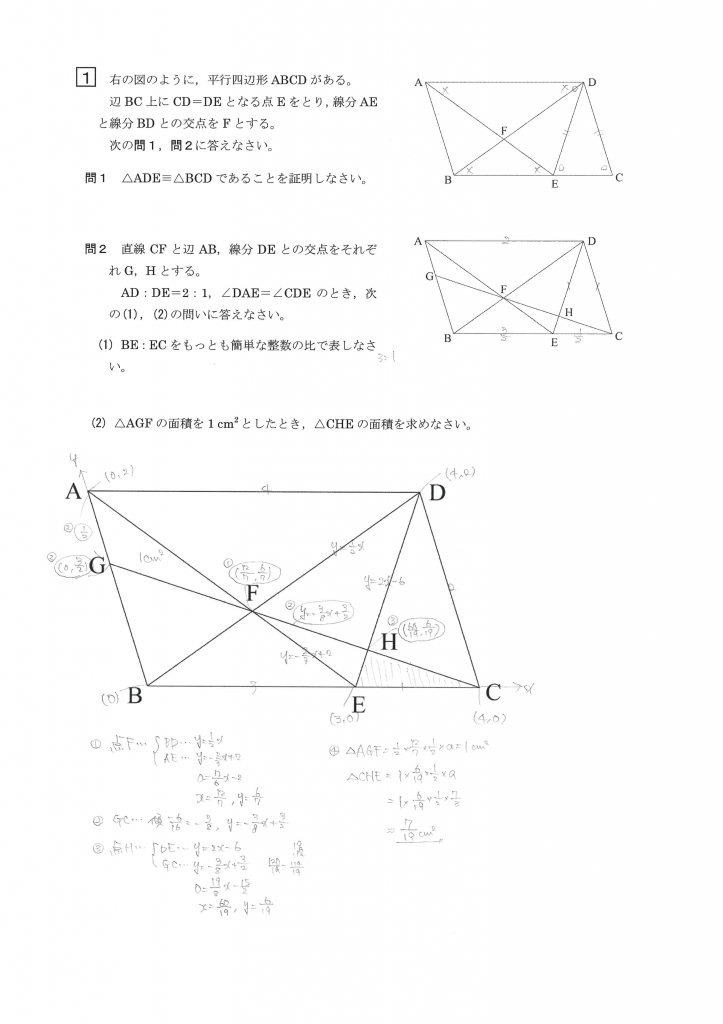
▲ 1次関数を使うメリットは「解き方の方向性を考える時間が０(ゼロ)である」という事。そして大抵とちゅうで「相似」に気づくという事。笑

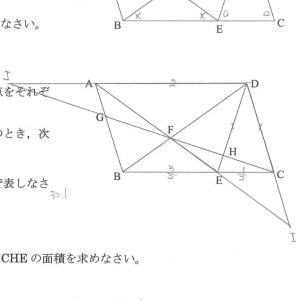
F-AG (BCに平行な長さ) は △AGF∽△ICF、H-EC (ABに平行な長さ) は △CHE∽△JHD で求められますね！ (*‘∀‘)/
主に中3SSクラスに通う生徒さんへ向けてのブログとなりましたが、みなさんには色々な解法を身につけてもらいたいです。 (*’ω’*)
理解の難しいようなら、自習室へ来てください。笑